A Integral Indefinida

Retornar

Definição1: Se F´(x) = f(x) então F(x) é uma primitiva de f(x).

Exemplo1: sen x  é uma primitiva de cos x  porque (sen x)´ = cos x.

Voltar ao Índice

Proposição1: Se F(x) é uma primitiva de f(x) e C é um número real então F(x) + C é também uma primitiva de f(x).

Ver demonstração

Voltar ao Índice

Proposição2: Se F(x) e G(x) são ambas primitivas de f(x) então existe um número real C tal que G(x) = F(x) + C.

Ver demonstração

Voltar ao Índice

Definição 2: O conjunto de todas as primitivas de f(x) é a integral indefinida de f(x) que é indicada por

f(x)dx

Pelas Proposições 1 e 2 temos que se F(x) é uma primitiva qualquer de f(x) então

f(x)dx

= F(x) + C, sendo que C percorre o conjunto dos números reais

Voltar ao Índice

Exemplo 2:	2.1) (arctg x)´=		logo,			dx = arctg x + C
	2.2) (arcsen x)´=		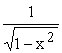logo,		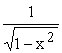	dx = arcsen x + C
	2.3) (arccos x)´= -		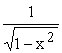logo,		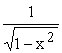	dx = -arc cos x + C

Compare os exemplos 2.2) e 2.3) !!!

Voltar ao Índice

Tabela de integrais  (provisória)

Inicialmente usaremos as seguintes integrais.

1)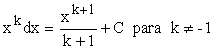

2)

dx / x =

ln|x| + C

(Ver justificativa)

3)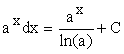

Caso paticular:

4)

cos x dx = sen x + C

5)

sen x dx = - cos x + C

6)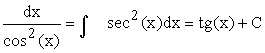

7)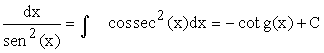
8)		tg(x).sec(x)dx = sec(x) +C
9)		cotg(x).cosec(x)dx = -cossec(x) +C

10)

dx = arctg x + C

11)		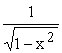	dx = arcsen x + C = - arccos x + C

13)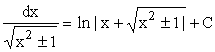

14)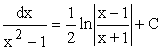

Voltar ao Índice

Propriedades da integral indefinida

1)

Para todo número real a diferente de zero,

a.f(x)dx = a.

f(x)dx .

2)

( f(x) + g(x) )

dx

=

f(x)

dx +

g(x) dx .

Voltar ao Índice

Exemplo 3:

+ 3.cos(x)

dx =

dx +

3

cos(x)dx =

arctg x + C1+

Voltar ao Índice

Demonstrações e justificativas

Demonstração da Proposição 1: ( F(x) + C)´= F´(x) + C´ = f(x) + 0 = f(x).

Voltar à Proposição 1

Demonstração da Proposição 2: ( G(x) - F(x))´= G´(x) - F´(x) = f(x) - f(x) = 0.

Logo, G(x) - F(x) é uma função constante, isto é,
existe um número real C tal que G(x) - F(x) = C.

Portanto G(x) = F(x) + C.

Voltar à Proposição 2

Justificativa de 2) :

Se x > 0, (ln | x | )´ =( ln ( x ))´= 1 / x.

Se x < 0, (ln | x | )´ =( ln (- x))´= -1.1/(-x) = 1/x.

Voltar a 2)

Voltar ao Índice

Retornar