A integral definida

 
Índice
Problema Definição 1 Proposição
Exemplo 2: Propriedades da 
integral definida		 Exemplo 3
Definição 2 Exemplo 4 Propriedade i)
Exemplo 5 Propriedade ii) 
O Teorema da  Média		 Definição 3 
- Valor médio
Propriedade iii) 
Construção de uma primitiva		 Exemplo 6 Propriedade iv)  
O Teorema fundamental do cálculo
Exemplo 7 Exemplo 8  

"Veremos o resultado mais importante do cálculo integral_ O teorema Fundamental do Cálculo".

"Não apresentaremos nenhuma demonstração para os resultados enunciados. Tais demonstrações são encontradas facilmente em livros sobre o assunto. Veja, por exemplo, nos livros  indicados nesse site".

Retornar

 Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) ³ 0 para todo x Î [a, b].

 

Problema: Calcular (definir) a área, A,

da região do plano limitada pela curva

y = f(x), o eixo OX e as retas x = a e x = b.

 

        Tomemos números x0, x1, x2, ..., xn Î [a, b] tais que a = x0 < x1< x2 < ... < xn = b e , a1, a2, ..., an tais que ai Î [xi-1, xi]. Então


 

Voltar ao Índice

 

Definição 1: Seja y = f(x) uma função definida e limitada no intervalo [a, b]. Se existe
 
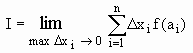
dizemos que f é integrável em [a, b] e que sua integral definida em [a, b] é I.

Notação:

 

Exemplo1: f(x) =3 para todo x Î [1, 2] 

 

 

De modo análogo, dada a função constante f(x) = C então

Voltar ao Índice

Proposição: Se f (x) é contínua em [a, b] então é integrável em [a, b].

Voltar ao Índice

 

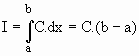
 Exemplo 2: f(x) = x para todo x Î [0, 1].

 

Mesmo sabendo tratar-se de uma função
que possui integral (pois é contínua), no momento ainda não temos recursos que facilitem calcular esta integral. Usaremos a definição e faremos uma escolha para os números x0, x1, x2, ..., xn  e  a1, a2, ..., an da seguinte forma: 

Dado n Î N tomemos 

Voltar ao Índice

 

Propriedades da integral definida

Se f(x) e g(x) são funções integráveis em [a, b] e k Î R então

        

        

        

 

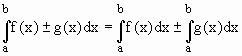
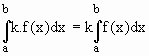
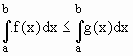
Casos particulares:

        Se f(x) £ 0, para todo x Î [a, b] então

      

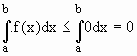
       Se f(x) ³ 0, para todo x Î [a, b] então

     

Voltar ao Índice

 

Exemplo 3:

Voltar ao Índice

 

Definição 2:

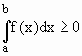
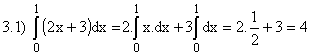
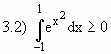
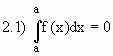
2.2) Se f(x) é integrável em [a, b] então

Voltar ao Índice

 

Exemplo 4:

 

Voltar ao Índice

 

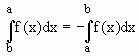
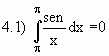
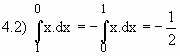
Outras propriedades da integral definida

 

Propriedade i) Sejam a, b, e c Î R, se

 

Voltar ao Índice

 

Exemplo 5:

Voltar ao Índice

 

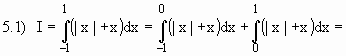
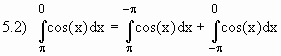
 Propriedade ii) - O Teorema da Média

Se f(x) é contínua em [a, b] então existe pelo menos um número c Î [a, b] tal que

" Se f(x) ³ 0, a área da região limitada pela curva y = f(x) e o eixo Ox é igual a área do retângulo de base [a, b] e altura f(c)"

Definição 3 ( Valor médio): f(c) é o valor médio de f em [a, b].

Voltar ao Índice

 

Propriedade iii) - (Construção de uma primitiva)

Se f(x) é contínua em [a, b] então

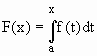
é uma primitiva de f(x). Isto é, F´(x)= f(x)

Voltar ao Índice

 

Exemplo 6:

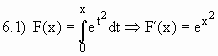
6.2) Calcular a derivada

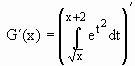
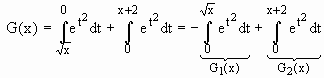
Se F(x) é a função dada em 6.1) então

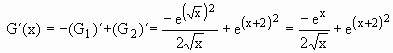
6.3) Estude o crescimento da função

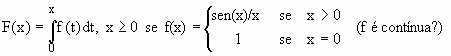
F´(x) = f(x) ³ 0 Û sen(x) ³ 0.

Portanto F(x) é crescente nos intervalos [2kp , (2k+1)p ] e decrescente em

[(2k+1)p , (2k+2)p ], k= 0, 1, 2

 

Voltar ao Índice

 

Propriedade iv) –O Teorema fundamental do cálculo

Se f(x) é contínua em [a, b] e F(x) é uma primitiva qualquer de f(x) então

Voltar ao Índice

 

Exemplo 7:

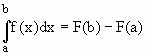
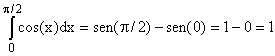
Notação:

Voltar ao Índice

 

Exemplo 8: Calcular o valor médio da função f(x) = 2x no intervalo [0, 1] e o ponto c Î

[0, 1] em que ele ocorre.

 

Voltar ao Índice

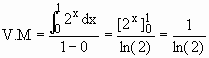
Retornar