Retornar
Mudança de variável na integral definida
|
Retornar |
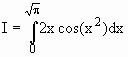
Usando mudança de variável na integral indefinida e o teorema fundamental do cálculo:
t = x2 Þ dt = 2xdx
![]()
![]()
Usando mudança de variável na integral definida:
t = x2 Þ dt = 2xdx
![]()
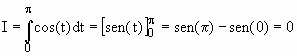
Dada a integral definida
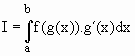
o procedimento prático para se aplicar mudança de variável é apresentado a seguir
t = g(x) Þ dt = g´(x)dx
x = a Þ t = g(a) e x = b Þ t = g(b)
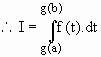
Este procedimento é baseado na seguinte proposição
Sejam J um intervalo e g: [a, b] ® J uma função com derivada contínua e f : J ® R uma função contínua. Então,![]()
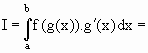
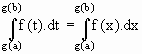
![]()
![]()
t = x +1 Þ dt = dx
x = -1 Þ t = 0 e x = 2 Þ t = 3
|
|
|
|
|
|
|
|
|
|
e tg(q ) = t/3 Þ t =3. tg(q )Þ dt = 3.sec2(q )dq e |
|
q = arctg(t/3), t = 3 Þ q = arctg(1) = p /4 e t = 0 Þ q = arctg(0) = 0 |
|
|
|
|
|
|
|
|
|
|
Integração por partes (integral definida)
Se u(x) e v(x) são funções definidas em [a, b] que possuem derivadas integráveis então,![]()
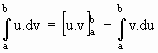
![]()
u = x Þ du = dx
dv = cos(x) Ü v = sen(x)
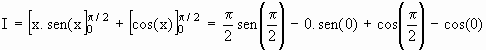
![]()
Outras propriedades da integral definida
| Se f(x) é uma função par e contínua em [-a, a] então |
|
|
|
![]()
![]()
![]()
|
|
|
|
Se f(x) é uma função ímpar e contínua em [-a, a] então
|
![]()
![]()
![]()
|
Se f(x) é uma função contínua em R e periódica de período T então para todo a Î R temos |
|
|
|
![]()
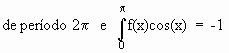 .
.
f(x).(cos(x) +sen(3x)) tem período 2p , então
![]()
f(x).sen(3x) é função ímpar e f(x)cos(x) é função par , então
![]()
Demonstrações
Se F(x) é uma primitiva de f(x), pelo teorema fundamental do cálculo
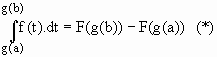
Pela regra da cadeia,
[F(g(x))]´= F´(g (x)).g´(x) e pelo teorema fundamental do cálculo
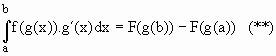
Com (*) e (**) fica demonstrada a proposição.
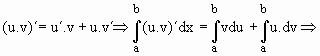
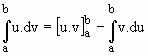
Demonstração da Propriedade i):
![]()
t = -x Þ dt = -dx e x = -a Þ t = a, x = 0 Þ t = 0 temos.
![]()
![]()
Demonstração da Propriedade ii) :
![]()
t = -x Þ dt = -dx e x = -a Þ t = a, x = 0 Þ t = 0 temos.
![]()
![]()
Demonstração da Propriedade iii):
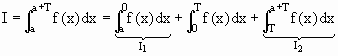
Vamos mostrar que I2 = - I1
![]()
t = x -T Þ dt = dx e x = T Þ t = 0, x = a +T Þ t = a temos.
![]()
Como f tem período T, f(t) = f(t + T), Logo
![]()
|
Retornar |