Sólidos de Revolução
Índice
Introdução Exemplo 1 Exemplo 2
Exemplo 3 Exemplo 4 Exemplo 5

 

 
 Introdução

Dados um plano a , um reta r desse plano e uma região R do plano a inteiramente contida num dos semi - plano de a determinado por r, vamos considerar o sólido de revolução gerado pela rotação da região R em torno da reta r.

.

Para isso usaremos ainda seções transversais e tomaremos como eixo orientado o eixo 
de rotação (a reta r).

Exemplo 1: Seja o triângulo, R, dado na figura ao lado. Calcular o volume do cone gerado pela rotação de R em torno do eixo OY.

Para cada y Î [0,1] a seção transversal ao eixo OY é um círculo gerado pela rotação do segmento horizontal de comprimento x (veja figura ao lado). Logo, possui área A = p x2 e o volume do cone é igual a

Usando semelhança de triângulos temos

Portanto

Voltar ao Índice

 

Exemplo 2: Seja a região R do plano limitada pela curva y = - x2 + 1 e o eixo OX. Determinar o volume do sólido obtido com a rotação de R em torno do eixo de OX.

A intersecção da curva com o eixo OX é dada por:  - x2 + 1 = 0 Û    x2 = 1 Û x = ± 1 e acima temos a representação gráfica da região R.  Para cada   x   Î [-1,1] a seção transversal ao eixo OX é um círculo gerado pela rotação do segmento vertical de comprimento y (veja figura ao lado). Logo, possui área A = p y2 e o volume do sólido é igual a

Portanto,



Voltar ao Índice


Exemplo 3: Seja a região R do plano limitada pelo eixo OY e pelas curvas

Determinar o volume do sólido obtido com a rotação de R em torno do eixo de OY.

Na figura acima temos representada a região R.
Como R é simétrica em relação OY , uma das duas regiões R1 ou R2 girando em torno de OY gera todo o sólido. Vamos considerar a região R1.

Para cada y Î [1/4 , 4] a seção transversal ao eixo OY é um círculo gerado pela rotação do segmento horizontal de comprimento x (veja figura acima) . Logo, possui área A = p x2 e o volume do sólido é igual a

Portanto,


Voltar ao Índice

  Clique na figura para ver animação da superfície em flash

Exemplo 4: Seja a ciclóide de equações paramétricas

4.1. Esboce a curva.

Usando as derivadas

obteremos a curva como apresentado ao lado.

4.2. Seja R a região do plano limitada pela ciclóide e pela reta y = -1. Determinar uma expressão em integrais que represente o volume do sólido obtido com a rotação de R em torno do eixo de OX.

Seja a função y = y(x) tal que seu gráfico   é    a ciclóide.   Para cada   x      Π  [-4p , 0] a seção transversal ao eixo OX é um anel circular de raio interno igual a 1 e raio externo igual a y (veja figura ao lado). Logo possui área igual a

A = p .y2 - p 12 = p .y2 - p e o volume do sólido é igual a

Substituindo x em função de t na integral acima temos

 

4.3. Determinar uma expressão em integrais que represente o volume do sólido obtido com a rotação de R em torno da reta x = 1

Sejam    as    funções   x1 = x1(y)   e   x2 = x2(y), funções cujos gráfico são respectivamente os arcos da ciclóide obtidos para t Î [p , 2p ] e para t Î [0, p ] (figura ao lado). Para cada y Î [-5 , -1] a seção transversal ao eixo OY é um anel circular de raio externo respectivamente é 1- x1 e 1 – x2   (figura abaixo).

 

 

 

Clique na figura para ver animação em flash

Logo, a seção transversal tem área A = p .(1- x1)2 - p (1- x2 )2 e o volume do sólido é igual a 

Substituindo y em função de t nas integrais acima temos


Voltar ao Índice

Exemplo 5: Calcular o volume do sólido gerado pela rotação, em torno do eixo OY,

do círculo de raio 1 e centro em (4,0 ) .

Tomemos as equações paramétricas do círculo:

Sejam x1 = x1(y) e x2 = x2(y), funções cujos gráfico são respectivamente os semi – círculos obtidos para t Î [-p /2, p /2] e para t Î [p /2 , 3p /2]. Para cada y Î [-1 , 1] a seção transversal ao eixo OY é um anel circular de raios externo e interno respectivamente iguais a x1(y) e x2(y). Logo, a seção transversal tem área A = p .x12 - p x2 2 e o volume do sólido é igual a

ou usando simetria

Substituindo por t temos

=

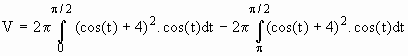Este sólido chama –se Toro.Veja sua representação gráfica a seguir

Clique na figura para ver animação em flash 4

Voltar ao Índice