Funções reais de n variáveis
|
| Retornar |
Definição 1: Chamamos de função real com n variáveis a uma função do tipo
f: D ® R com D Ì Rn = R ´ ....´ R.
Ou seja, uma função cujo domínio D (ou D(f)) é um subconjunto de Rn e seu contra-domínio é R.
1.1 f: R2 ® R
(x , y) |® 2x + 3y
D = R , é uma função real de duas variáveis.(é também uma função linear)
1.2 f: R3 ® R
(x, y, z) |® x2 + 3y +z
D = R3, é uma função real de três variáveis (é também uma função polinomial)
1.3 f : R3 – { (0,0,0) }® R
D = R3 – { (0,0,0) } Ì
R 3 é uma função real de três variáveis. (é
também uma função racional, isto é,
quociente de duas funções polinomiais)
Usamos, também, a notação ( mais resumida) para representar funções reais de n variáveis;
y = f ( x1, ....., x n)
Neste caso D (f ) é o conjunto D ( f ) = {(x1,
..., x n) 
Rn; f (x1,...., x n)
R }
Exemplo 2: Determine e represente geometricamente os domínios das funções
2.1 f (x, y) = 3x 2 + 1
D (f ) = R2
Representação gráfica
Figura 1 |
x 2 + y 2 + 1 = 0, não tem solução, logo D (f ) = R 2.
Representação gráfica: Figura 1
x 2 + y 2 = 0. Como x 2 
0 e y 2 0 então x 2
+ y 2 = 0 
x 2 = 0 e y 2 = 0 x = 0 e y = 0.
Logo D(f ) = R 2 – {(0,0)}.
Representação gráfica
D (f ) = {(x, y) R
2; x – y 
0}, ou seja, todo o plano exceto a 1a
bissetriz.
Representação gráfica
D (f ) = {(x, y) R
2; x 2 > y}
Representação gráfica
Tomemos a parábola y = x2 (figura a seguir). Fixando x = x0 , a solução da inequação
x02 > y é o conjunto de todos os pontos da reta x = x0 situados abaixo do ponto (x0, x02) da parábola. Portanto D(f) é a região do plano abaixo da parábola.
 |
D(f)
|
Representação gráfica
equivalente a x – y > 0 e y – 1 > 0 ou x - y < 0 ou y – 1 < 0. Vamos então estudar o sinal de cada um dos termos x – y e y –1.
x - y:
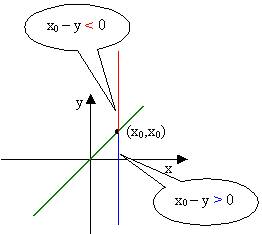
Seja a reta x – y = 0 (figura a seguir). Fixando x = x0 , a solução da inequação
x0 – y > 0 é o conjunto de todos os pontos da reta x = x0 situados abaixo (observe que o coeficiente de y é menor que 0) do ponto (x0, x0) (da reta x – y) . Da mesma forma a solução de x0 – y < 0 é o conjunto dos pontos da reta x = x0 acima do ponto (x0, x0)
 |
|
y –1: O sinal deste termo está indicado na figura a
seguir
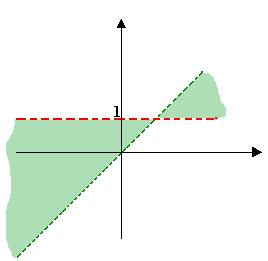
Na figura a baixo temos a representação gráfica de D(f)
D(f) = {(x,y) Î R2; x2 + y2 £ -1 ou x2 + y2 ³ 1}, ou melhor, como x2 + y2 £ -1 não ocorre para nenhum (x,y) Î R2, D(f) = {(x,y) Î R2; x2 + y2 ³ 1}.
Representação gráfica
(x,y) é tal que x2 + y2 ³ 1 se, e somente se, a distancia deste
ponto à origem é maior ou igual a 1.
Logo D(f) é a região do plano formada pelo círculo e por seu
exterior.
D(f)
Representação gráfica
Tomemos a elípse
x02 + y2/4 -1 £ 0 do 2o grau em y, cujas raízes da equação correspondente são
é o conjunto de todos os pontos da reta x = x0 iguais ou situados entre os pontos da elípse
Portanto D(f) é a região do plano que inclui a elipse e seu interior
 |
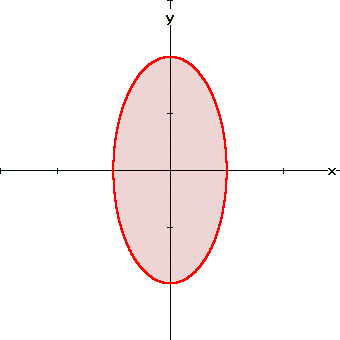 D(f) |
Gráfico
Definição 2: Dado uma função f: D ® B seu gráfico é o conjunto {(a, f (a);
a D}.
No caso de funções reais de uma variável temos:
f: D ® R; D Ì R seu gráfico é uma curva do R2.
Para uma função de duas variáveis
f: D ® R, D Ì R 2
(x, y) ® f (x, y)
O gráfico da função f é uma superfície de R3.
Exemplo 3: A esfera x 2 + y 2 + z 2 = 1 é uma superfície de R3 que não é gráfico de função z = f(x,y).
Da equação da esfera tem-se,
D (f) = D (g) = {(x, y) R 2; x 2 + y 2 £ 1} (O círculo x 2 + y 2
= 1 e seu interior)
O gráfico de f é a semi-esfera superior (z ³ 0) e o gráfico de g é a semi-esfera inferior
(z £ 0).
Curvas de nível
Um recurso auxiliar para esboçar gráficos são as curvas de nível da função.
Definição 3: Dados uma função z = f (x, y) e
k Î R , a curva de nível de f em z =
k é o
conjunto { ( x, y ) Î R2;
f ( x, y) = k }. Ou seja, é o conjunto dos elementos do domínio
de f
que possuem imagens igual a k. É também a intersecção do
gráfico de f com o plano
(paralelo a XOY ) de equação z = k
Exemplo 4: Determine e esboce a curva de nível de f (x, y) = y/x em z = 2.
A curva de nível é o conjunto dos pontos ( x, y ) Î R2 que satisfazem a
2 = y/x Û y = 2x com x ¹ 0. Ou seja, trata-se da reta de equação y =2x exceto o ponto (0,0)
Representação gráfica:
Exemplo 5: Dada a função
determine e represente seu domínio e as suas curvas de nível.
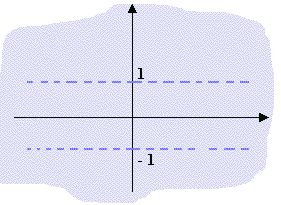
D(f) = {( x, y ) Î R2; y ¹ -1 e y ¹ 1 } (ou seja, todo o plano exceto as retas y = 1 e y = -1).
Representação gráfica
Curvas de nível
Seja a equação x/(y2 –1) = k que é equivalente a x = k(y2 –1 ) com y ¹ 1 e y ¹ -1 .
Para k ¹ 0, temos a parábola x = k(y2 –1) com exceção dos pontos (0, -1) e (0, 1 )
Para k = 0 temos x = 0 com y ¹ 1 e y ¹ -1 , ou seja, o eixo OY exceto os pontos (0,1) e (0, -1).
Representação gráfica:
|
|
k ³ 0 |
k < 0 |
|
| Retornar |
