Retornar
Integrais de Funções Racionais
|
Retornar |
| Definições: |
| 1) Uma
função polinomial é uma função da forma f(x) = anxn + an-1xn-1 + ... + a1x + a0 tal que an, an-1, ... a1, a0 Î R. Se an ¹ 0, seu grau é igual a n. |
| 2) Uma função racional é uma função da forma f(x) = p(x)/q(x) com p(x) e q(x) funções polinomiais e q(x) ¹ 0 (isto é, não é a função identicamente nula) |
 |
![]()
É racional própria, porque o grau do numerador é menor do que o grau do denominador.
![]()
É racional imprópria, porque o grau do numerador é igual ao grau do denominador.
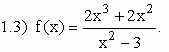
É racional imprópria, porque o grau do numerador é maior do que o grau do denominador.
Definição 3: Uma função racional f(x) = p(x)/q(x) é,
3.1) Própria grau [p(x) ] < grau[q(x)]
3.2) Imprópria se grau[p(x) ] ³ grau[q(x)] ou p(x) é a função identicamente nula.
Exemplo 2: Toda função polinomial é uma função racional imprópria.
![]()
| Integrais de funções impróprias |
| No cálculo da integral de uma função racional imprópria (dividindo-se o numerador pelo denominador) escreve - se a função como soma de uma função polinomial e uma função racional própria. |
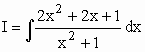
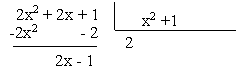
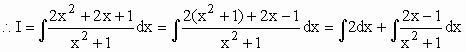
![]()
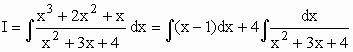
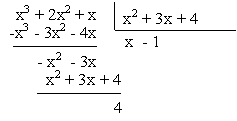
Continue! (Veja aula anterior)
![]()
Usando integração por partes
u = arctg(x) Þ du = dx/(1 + x2)
dv = x Ü v = x2/2
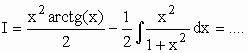
Continue! (A última integral é imprópria)
São frações parciais funções da forma:
ax2 + bx + c não possui raízes reais)
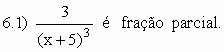

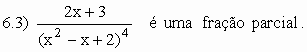
![]()
t = x + 5 Þ dt = dx
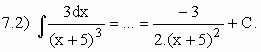
t = x + 5 Þ dt = dx
| Veja aula anterior. |
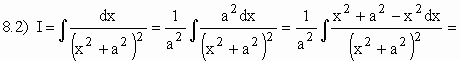
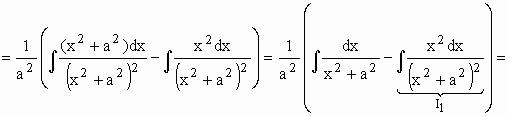
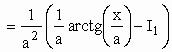
Usando integração por partes para calcular I1 ...
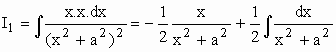
u = x Þ du = dx
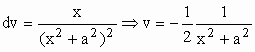
![]()
| Portanto | I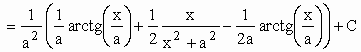 |
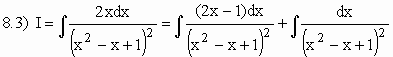
t = x2 – x + 1 Þ dt =(2x – 1)dx
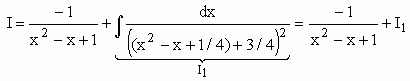
Calculando I1 ...
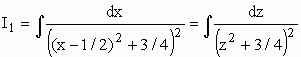
z = x – 1/2 Þ dz = dx
Aplicando o mesmo método do exemplo 8.2) para
a = ![]() ..
..
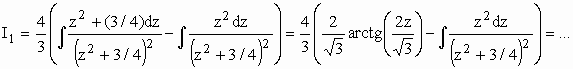
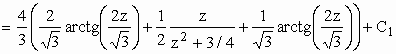
Portanto,
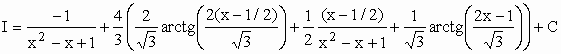
|
Retornar |