Integrais de funções próprias

Integrais de funções racionais próprias

Método da decomposição em frações parciais

Como já vimos, toda integral de função racional pode ser escrita como soma de uma integral de função polinomial e uma integral de função racional própria. Portanto, com um método para resolver integrais das racionais próprias, podemos calcular integrais de quaisquer funções racionais.

Esse método consiste em escrever uma função racional própria como soma de frações parciais que dependem, principalmente, da fatoração do denominador da função racional em R .

Índice
Exemplo 1. 1	1^o Caso	Exemplo 1. 2	Exemplo 1. 3
Exemplo 2 . 1	2^o Caso	Exemplo 2. 2	Exemplo 3 . 1
3^o Caso	Exemplo 3 . 2	Exemplo 4 . 1	4^o Caso
Exemplo 4 . 2

Retornar

Seja f(x) = p(x)/q(x) tal que p(x) e q(x) são funções polinomiais com grau[p(x)] < grau[q(x)] .

1^o Caso:

Exemplo 1.1:

É racional própria.

D > 0, não é fração parcial.

x² – 4 = (x – 2)(x + 2)

Decompondo em frações parciais...

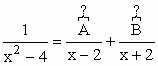
1= A.( x + 2) + B.(x – 2) = (A+B)x +(2A – 2B)

Pela igualdade acima entre funções polinomiais temos

A + B = 0 e 2A – 2B =1 Û A = 1/4 e B = -1/4

Ainda usando a igualdade das funções polinomiais, podemos calcular A e B atribuindo valores a x:

x = 2:

1 = A.( 2 + 2) + B.(2 – 2) Þ 1 = 4.A Þ A = 1/4

x = -2:

1 = A( -2 + 2) + B.(-2 – 2) Þ 1 = -4.B Þ B = 1/4

Obs. Podemos atribuir quaisquer valores a x, inclusive as raízes de q(x) que facilitam a tarefa de calcular as constantes.

Voltar ao ìndice

1^o Caso:

Se todas as raízes de q(x) são reais e simples (isto é, duas a duas distintas).

Neste caso, se a₁, a ₂, ... a_nsão as raízesde q(x) então

q(x) = M.(x - a₁). (x - a ₂)... (x - a _n) e

Voltar ao ìndice

Exemplo 1.2:

É racional própria.

x³ – 4x + 3x = x.(x – 1)(x – 3) (*)

Decompondo em frações parciais...

De (*) e ( **) segue-se que 1 = A(x - 1)(x - 3) +Bx.(x – 3) + Cx(x –1)

Atribuindo valores a x:

x = 0:

1 = A(0 - 1)(0 - 3) + B.0.(0 – 3) + C.0.(0 –1)

Þ 1 = 3.A Þ A = 1/3

x = 1:

1 = A(1 - 1).(1 - 3) + B.1.(1 – 3) + C.1(1 –1)

Þ 1 = -2.B Þ B = -1/2

x = 3:

1 = 6.C Þ C = 1/6

Voltar ao ìndice

Exemplo 1.3:

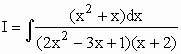
É racional própria.

(2x² – 3x + 1)(x + 2) = 2(x - 1/2).(x – 1)(x + 2) (*)

Decompondo em frações parciais...

( **)

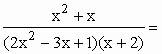
De (*) e ( **) segue-se que

(x² + x) = 2(A(x - 1)(x + 2) +B(x –1/2).(x + 2) + C(x –1/2)(x –1))

Continue!

Voltar ao ìndice

2^o Caso:

Exemplo 2.1:

É racional própria.

x.(x² – 2x + 1)= x.(x – 1)² (*)

Decompondo em frações parciais...

De (*) e ( **) segue-se que x + 2 = A(x - 1)² + Bx.(x – 1) + Cx

Atribuindo valores a x:

x = 0:

A = 2

x = 1:

C = 3

x = 2:

4 = A (2 - 1)² +B.2.(2 – 1) + C.2 Þ 4 =A +2.B + 2.C Þ 4 = 2 + 2.B + 2.3 Þ B = -2

Voltar ao ìndice

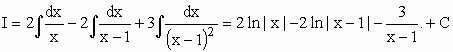
2^o Caso:

Se todas as raízes de q(x) são reais.

Neste caso se a ₁, a ₂, ... a _nsão as raízesde q(x) com multiplicidades k₁, k₂, ..., k_n então q(x) = M.(x - a ₁)^k₁. (x - a ₂)^k₂... (x- a _n)^k_n e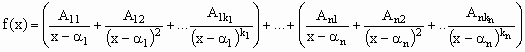

Voltar ao ìndice

Exemplo 2.2:

É racional própria.

x⁴ – 8x² + 16 = (x²)² – 8x² + 16 = (x²)² – 8x² + 16 = (x² – 4)² =

= (x – 2)².(x + 2)² (*)

Decompondo em frações parciais...

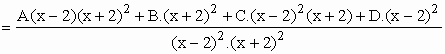De (*) e ( **) segue-se que

1 = A(x - 2)(x + 2)² +B.(x +2)² + C(x –2)² .(x + 2) + D.(x – 2)² Þ

Igualando os coeficientes das funções polinomiais ...

Coef de x³: A + C = 0

Coef de x²: -2A + 4A + B + 2C – 4C + D = 0

Coef de x: 4A – 8A + 4B + 4C – 8C - 4D = 0

Termo ind: -8.A + 4B + 8.C + 4.D = 1

Resolvendo o sistema obtém-se

A = -1/32; B = 1/16; C = 1/32; D = 1/16.

Voltar ao ìndice

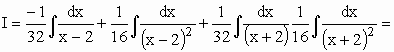
3^o Caso:

Exemplo 3.1:

É racional própria.

x³ + 1= (x + 1).(x² – x + 1) (Observe que x² – x + 1 não possui raízes reais) (*)

Decompondo em frações parciais...

( **)

De (*) e ( **) segue-se que 1 = A(x² – x +1) +(Bx +C).(x + 1)

Atribuindo valores a x:

x = -1:

A = 1/3

x = 0:

C = 2/3

x = 1:

B = -1/3

t = x² – x +1 Þ dt = (2x –1)dx

Voltar ao ìndice

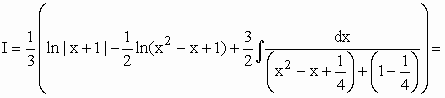
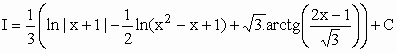
3^o Caso:

Se todas as raízes não reais de q(x) são simples (isto é, duas a duas distintas).

Neste caso, se a ₁, a ₂, ... a _nsão as raízesreais de q(x) com multiplicidade

k₁, k₂,..., k_n e

são suas raízes não reais então

q(x) = M.(x - a ₁)^k₁. (x - a ₂)^k₂... (x- a _n)^k_n (x² +b₁x +c₁) ... (x² +b_mx +c_m)e

tal que, para todo j = 1...m, x² +a_jx +b_j é um polinômio com coeficientes reais e com raízes (não reais)

Voltar ao ìndice

Exemplo 3.2:

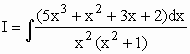
É racional própria.

x² + 1 não possui raízes reais

Decompondo em frações parciais..
.

Segue que 5x³ + x² + 3x + 2 = A.x.(x² +1) +B.(x² +1) +(C.x + D).x²

Igualando os coeficientes...

Coef de x³: A + C = 5

Coef de x²: B + D = 1

Coef de x: A = 3

Termo ind: B = 2

Logo,

A = 3 ; B = 2 ; C = 2; D = -1.

Continue!

Voltar ao ìndice

4^o Caso:

Exemplo 4.1:

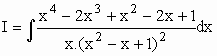
É racional própria.

Decompondo em frações parciais...

Segue-se que

x⁴ - 2x³ + x² –2x +1 = A(x² – x +1)² +(Bx +C).x.(x² –x + 1) + (Dx + E)x

Igualando os coeficientes...

Coef de x⁴: A + B = 1

Coef de x³: -2A – B + C = -2

Coef de x²: 3A - C + B + D = 1

Coef de x: -2A + C + E = -2

Termo ind: A = 1

Logo,

A = 1 ; B = 0 ; C = 0; D = -2; E = 0.

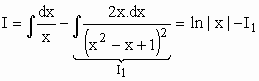
Veja resolução de I₁ no exemplo 8.3 da aula anterior .

Voltar ao ìndice

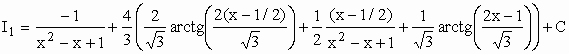
4^o Caso: Caso geral (para qualquer polinômio real q(x) ¹ 0).

Neste caso, se a ₁, a ₂, ... a _nsão as raízesreais de q(x) com multiplicidade

k₁, k₂,..., k_n e são suas raízes não reais com

multiplicidade s₁, s₂, ..., s_mentão q(x) = M.(x - a ₁)^k₁. (x - a ₂)^k₂... (x- a _n)^k_n (x² +b₁x +c₁)^s₁ ... (x² +b_mx +c_m)^s_me

tal que, para todo j = 1...m, x² +a_jx +b_j é um polinômio com coeficientes reais e com raízes (não reais)

Voltar ao ìndice

Exemplo 4.2:

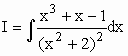
É racional própria.

Decompondo em frações parciais.

..

Segue-se que

x³ + x - 1 = (Ax + B).(x² + 2) + (Cx + D)

Igualando os coeficientes...

Coef de x³: A = 1

Coef de x²: B = 0

Coef de x: 2A + C = 1

Termo ind: 2B + D = -1

Logo,

A = 1 ; B = 0 ; C = -1; D = -1.

Continue ....

Voltar ao ìndice

Retornar