Curvas parametrizadas
- Continuação –
| Retornar |
Exemplo 1: Calcular a área da região do plano limitada pelo eixo OX, pelas retas x = 0 e x = 8 e pela curva C de equações paramétricas.
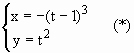
Podemos interpretar as equações da curva C como equações do movimento de um ponto sobre o plano, isto é, (x(t), y(t)) dá a posição do ponto no instante t. x(t) nos dá o movimento na horizontal e y(t) nos dá o movimento vertical. Usaremos então os sinais das derivadas
![]()
para obter o crescimento e decrescimento de x e de y em relação a t.
Quanto a concavidade da curva, para efeito das aplicações que vamos fazer, não é necessária.
Temos,
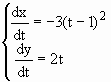
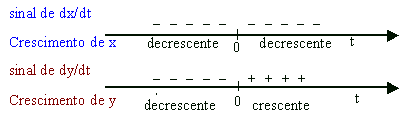
Pelas equações (*)
![]()
Calculando as intersecções entre as curvas:
Pelas equações (*) ,
x = 0 Þ 0 = -(t-1)3 Þ t = 1
x = 8 Þ 8 = -(t-1)3 Þ t = -1
Contando apenas com estas informações podemos apresentar a seguinte representação gráfica para a área
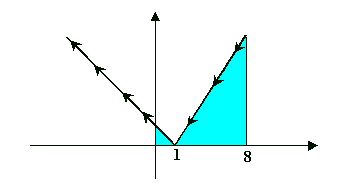
As setas indicam o sentido em que a curva C é percorrida.
Observe que este gráfico não indica corretamente a concavidade da curva C (é bastate imperfeito!), mas, no momento, serve aos nossos propósitos.
Seja y = y(x) a função cujo gráfico é a curva C. Então
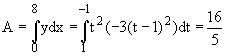
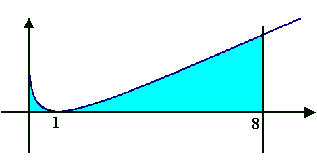
O gráfico a seguir representa a curva com mais exatidão.
Exemplo 2: Dado a > 0, calcular a área da região do plano limitada pelo eixo OX e pela curva C de equações paramétricas
![]()
Temos,
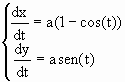
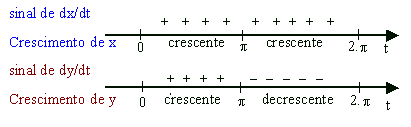
Pelas equações (*)
![]()
![]()
![]()
Apenas com estas informações podemos apresentar a seguinte representação gráfica para a área.
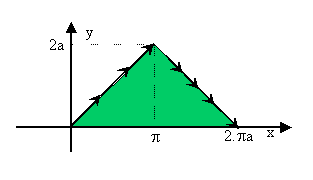
Seja y = y(x) a função cujo gráfico é a curva C. Então
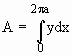
Com a mudança de variável
![]()
![]()
x = 0 Þ t = 0; x = 2p a Þ t = 2p , temos

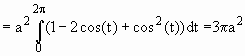
De fato essa curva é chamada ciclóide e tem a seguinte representação gráfica.
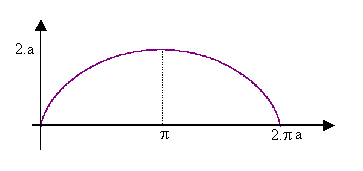
Clique na figura para obter mais
informações sobre a ciclóide
Exemplo 3: Calcular a área da região do plano limitada pelo pelo laço da curva C de equações paramétricas
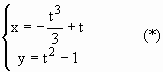
Temos,
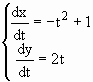
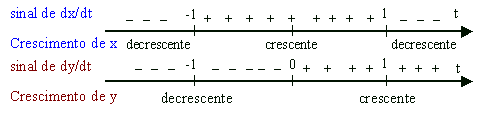
Pelas equações (*)
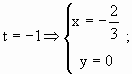
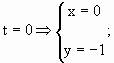
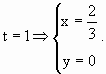
Usando apenas estas informações podemos apresentar a seguinte representação gráfica para a área.
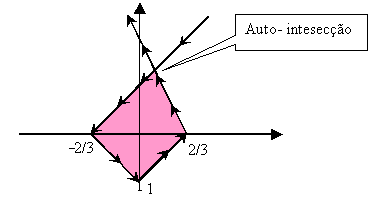
É preciso calcular o ponto de auto-intersecção da curva, que é um ponto por onde o móvel passa duas vezes (ou seja em dois instantes diferentes) . Logo, sejam t1 < t2 tais que x(t1) = x(t2) e y(t1) = y(t2).
y(t1) = y(t2) Þ (t1)2 –1 = (t2)2 –1 Þ t1 = ± t2 Þ t1 = - t2 .
![]()
![]()
t2 = 0 Þ t1 = t2 (não serve!).
![]() .
.
Temos,
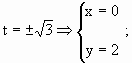
Sejam A1, A2, A3 e A4 as áreas indicadas na figura abaixo. Temos A = A1 + A2 + A3 +A4
Se y1 = y(x), y2 = y(x), y3 = y(x), y4 = y(x) são as funções cujos gráfico estão indicados na também na figura abaixo
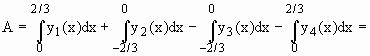
Fazendo a mudança de variável,
![]()
temos,
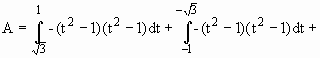
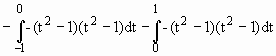
![]()
|
|
|
|
A figura acima é uma representação gráfica mais exata para a curva C |
| Retornar |